Pausing to recapture our flow
We have covered a lot of ground so far in Lazarus Math. Since you are reading this, that means you have persisted. Let me take a quick pause in our journey to reorient our perspective before we jump into more math stories.
As you know, the purpose for Lazarus Math is quite different from the purpose for other math material. The focus for Lazarus Math is more difficult to explain because it is not as concrete as learning how to solve a quadratic equation. We’ve referred to this difference as precision versus vision.
It is easy to explain the output of a precision strategy: follow these steps and you can solve the quadratic equation. You know you have arrived if you get to the right answer.
The output we want for vision is more difficult to measure. I don’t have a test to determine whether your vision is on the right track. But I did think of an example in my life that may be helpful in clarifying our goal.
My parents told me that when I was a baby, all I wanted to do was to play with a ball. I was never interested in things like trucks or other toys. For me, I was drawn like a magnet to anything that you could throw. Because my dad was a basketball coach, the first sport I started with was basketball. My dad said that even when I was three, I could sit and watch a 2-hour basketball game and not be distracted. As soon as I was big enough, I was shooting basketballs. After a while, I got pretty good at it. Even though my dad was a basketball coach, I don’t remember him ever teaching me how to shoot a basketball. I just let my instincts take over and practiced. I always seemed to have a basketball with me.
I remember my sister asking me to go running with her, so I naturally took a basketball with me and dribbled along the way. I learned basketball by trusting my instincts and playing. Unfortunately, I lacked athletic ability (think running and jumping) so my basketball career ended in high school. But I became quite proficient at doing things with a basketball.
Fast forward to my adult years and I decided golf was a good sport to pick up as the body ages. I figured that I could take the passion I had for basketball and apply it to a golf swing and get good at it. I had dabbled in golfing for about 40 years, but I wasn’t good at it because I swung the golf club like a baseball bat, which is natural because baseball was my second sport passion as a kid. But, after 40 years of swinging the golf club the wrong way, I figured I could learn the right way. I was optimistic I could learn to swing the golf club correctly because we are in an enlightened age where there are tons of YouTube videos available for me to learn how to swing a club.
So the natural thing for my analytical mind to do was to watch the videos to learn how to swing a golf club. When you break it down, there are so many steps to successfully hit a ball. When I went to practice, I had about 10 things in my mind that I was working on. As a result, I was dividing the swing into these 10 different components that I was trying to accomplish in the short time it takes to swing a golf club.
Despite a year and a half of dedicated practice, the swing has not yet “clicked.” Of course, this baffles me because I know I learned other athletic skills such as shooting a basketball. Why can’t I learn to swing a golf club like I shoot a basketball? I’ve come to the conclusion that my approach to learning to swing a golf club needs to be more like how I learned to shoot a basketball.
I need to stop thinking about the discrete steps and allow the swing to naturally flow as my body hits the golf ball. Yes, there are elements of a swing that need to be in place. But my experience is that you can destroy a process by trying to focus on the steps.
Isn’t that true of the bigger picture of life? The idea of a continuous flow is what life is all about. We need to know a few things to ride a bicycle. But the main thing is to get on the bike and be willing to fall. We learn to ride a bike not by following certain steps but by practice and persistency. This is also true of things in life other than physical ability.
Sure, we may go through some basic steps to follow before we get married. But the goal for a good relationship is not the ability to succeed at following certain steps. It is the ability to have a smooth flow. To me, a measure of “success” is when we achieve this continuous flow without our mind thinking about the steps.
This idea of a continuous flow is at the heart of why I wrote Lazarus Math. There are plenty of resources that teach you different steps to solving math problems. But what I’ve experienced in math is the continuous flow. I see math in life. It is everywhere. I am intrigued by interesting problems. I am no longer conditioned to want to find “the answer” in the back of a math book.
I approach math in a similar way to how I approached basketball as a kid. I am always playing with it. I learn as I do. Sure, I am always learning new “steps” as I consume and practice math. But I never think of it as steps. I think solving math problems requires a similar skill to shooting a basketball. You learn some basic fundamental principles (logic, reasoning, etc.) but you trust that you have an innate ability to do math.
Is your math flowing?
Lazarus Math is all about math coming alive inside of you. Hopefully, you are seeing that this life already exists inside of you. Sometimes we need to return to a childlike perspective of playing with things that our adult mind may think we do not have the capacity to do.
I think it is unfortunate that we live in a culture where most adults view themselves as not having natural math ability. It is easy to see why they have that perspective because they have “fallen off the bike” so many times in terms of struggling to truly understand math concepts. I think so much attention has been given to the steps to solve problems and not enough attention to letting our curious mind play with an idea and give it space to wrestle.
A math dance
With all that said, let’s journey forward to our next adventure. Our next math story is about truly amazing math. It involves some of the best ideas from some of the best minds of math. Many people have struggled to follow the math, so I’m trying a different approach. I’m going to package our next math nugget into a story about dancing.
Dancing is like the other things that I mentioned where the goal is to develop a flow. Good dancers view dancing as a continuous process, not a set of discrete steps. I do recognize that there are steps in this math that must be discussed. I’m presenting this math in a dance story to hopefully make it interesting. In this story, however, I’m going to walk you through the steps in detail. The reason why I’m walking through the detailed steps is because I want it to seem intuitive to you. Each step is small so you can be confident that you can achieve it. But in the end, we will again appeal to the continuous flow of math. The hope is you will understand the process at the end so that you will no longer need to do the steps.
Our first dance
Before we jump into the steps, let’s focus on a beautiful dancer whose movements graciously flow with the music. That is the picture of where we want to be with the math at the end of this section. We will build up to the final dance by starting with easier dances. I call our first dance the “Straight 1” dance.
All moves in our Straight 1 dance travel in the same direction. First, move a distance 1. As usual, we don’t care what the unit is for distance. I suppose a reasonable unit for this dance is 12 inches or a foot. We won’t worry about that detail as we imagine dancing with math.
Our second move is a distance , which is also 1. Next, move a distance , which is . Then, move a distance , which is . Follow this movement pattern for as long as you can. The question is: how far would you have moved if you performed this dance forever? Clearly, each move covers much less distance than the previous move, except for the first two moves which were both 1.
We’ll chart the dance on a number line. Since we are using a number line, we will use the normal convention of moving left to right. Figure 1 is a graph of the distance we traveled.

Figure 1. Straight 1 dance
Before we get to the answer, let’s identify a pattern to our steps. First, we have a shortcut for writing each term in the denominator. Recall our factorial function when we explored the gamma function. We get the opportunity to spring this function into action. If we input an unknown integer , we write , which is . Recall by definition. That means we can rewrite the 1st term as , the 2nd term is , and the 3rd term is . If you follow the pattern, the th term is. It is an interesting pattern of steps which is visualized in Figure 2.
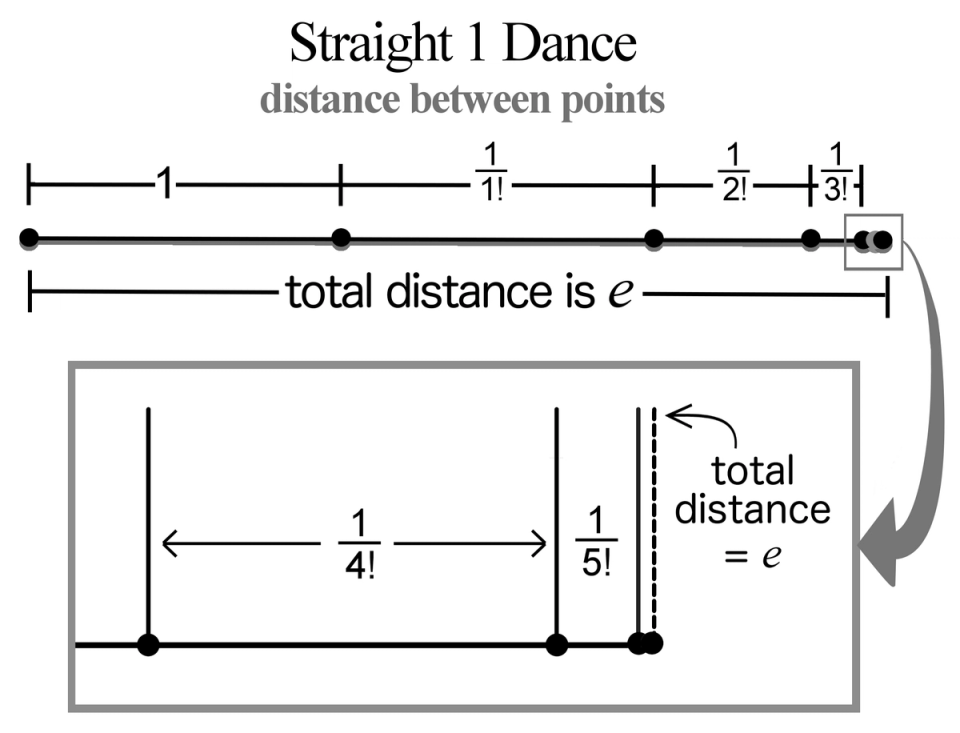
Figure 2. Straight 1 dance finish
Our key question is: how far did we travel in our dance? The distance we traveled if we performed the steps an infinite number of times (let approach infinity) is approximately 2.718281828459045. Of course, the exact value is none other than . Isn’t that fun? Was it a surprise that the total distance we traveled simplified to ? There is a lot of math to unpack with this formula by moving to our second dance.
Our second dance
I refer to our second dance as the Straight 2 dance. If you liked Straight 1, then you’ll like Straight 2 assuming your body can move farther. Again, every move is in a straight line. Like before, the first move covers a distance of 1. But this time, the second move covers a distance of 2. The third move covers a distance of , and the fourth . Do you recognize the pattern? It may help to rewrite the first two moves as and . Thus, the th step in our Straight 2 dance is to move a distance of , which you can see in Figure 3.
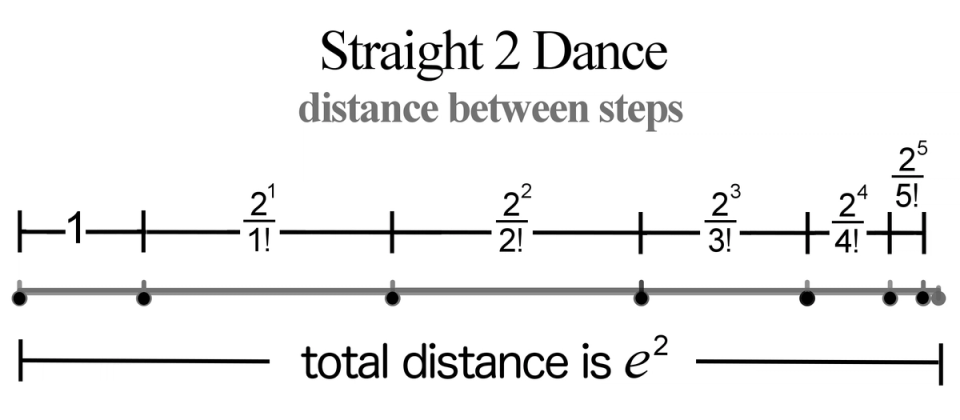
Figure 3. Straight 2 dance
In the end, how far have we moved forward as approaches infinity? This time, we moved approximately 7.389056098930649, which is exactly . Who thought dancing could be so fun!
Our dance
In our Straight 1 dance, the distance we traveled in our th step is . A nice trick with 1 is that multiplying by itself does not change the value, so we can instead say the distance of our th step is . The total distance traveled after infinitely many steps is .
In our Straight 2 dance, the distance we traveled in our th step is and the total distance traveled is . Do you recognize the pattern?
Consider the moves for the Straight dance where can be any positive integer. If we follow the pattern, the distance we travel in the th step of our Straight dance is .
Our dance research is paying dividends because we can quickly identify the total distance we travel in other dances where is a positive integer. For example, we can define a Straight 4 dance by writing . Then, the total distance we travel forward in this dance after an infinite number of steps is , or about 54.6.
Does this dance pattern still work if we journey off the positive integers and move to something like Straight 3.5? For example, is ? The pattern we hope for, in fact, exists. If we let , our distance traveled as approaches infinity is exactly . We show the length of the first 6 steps and the total distance in Figure 4.
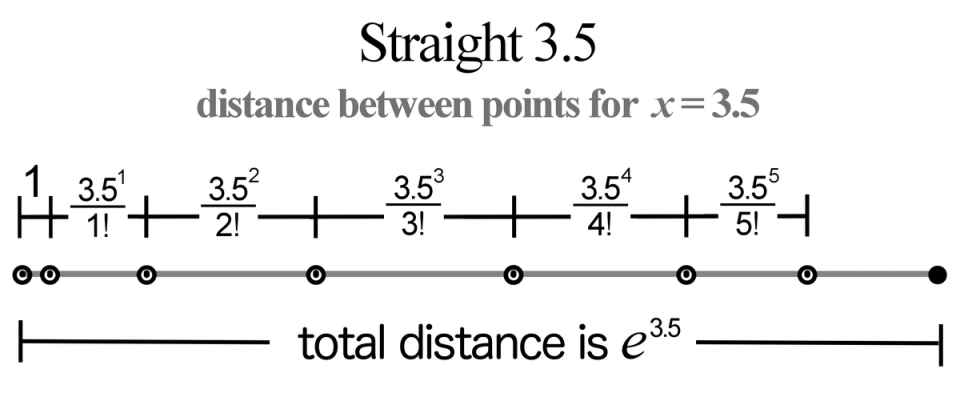
Figure 4. Straight 3.5 dance
Wonderful! Don’t you feel a calming sense of order to our dance since our dance pattern not only works for positive integers but also for positive real numbers?
Dancing with the negatives
Since we have this calming sense of order, maybe we are feeling bold enough to ask if this pattern also works for negative real numbers. Perhaps we don’t comprehend how bold our question is. At first, it seems like a small request. Just put a negative sign in front of 3.5 and crank out the dance. Let’s try the Straight -3.5 dance and discover what chaos we just created.
Because of the disturbance we are about to create, let’s use a full-blown number line to monitor this new dance. Again, start at 0. Our first step is the familiar step of distance 1. We’re still moving left to right as we did before. We can see that we land on the point 1 on the number line.
OK, where do we go for step 2? Remember the formula. In step , we move That means in step 2, we let . Also, this is our dance for , so let . That means the distance we travel in step 2 is . On a number line, we’re conditioned to think a negative value represents going right to left, so do a half turn and step 3.5 in the opposite direction. Now, we rest at the point .
Fine, we can do this. But where do we go next? Our next step is for which covers a distance of . Perhaps you recall we have this strange rule in math that if you multiply two negative numbers, you get a positive number. That’s what we have here with . If we punch this into a calculator, we get the distance traveled in step 3 is 6.125. Since this is positive, do another half turn and dance 6.125 in the positive direction. Because we started step 3 at -2.5, we finish step 3 at the location .
Notice the distances for each step is the same distance we performed for the Straight 3.5 dance. The only difference is in the Straight 3.5 dance we danced in only one direction. Thus, the only thing we’ve introduced here is a half turn after each step. However, we still don’t know where we will eventually land. Let’s pick up our pace and identify the next several steps.
Step 4: Distance traveled = . Finish at .
Step 5: Distance traveled = . Finish at .
Step 6: Distance traveled = . Finish at .
Step 7: Distance traveled = . Finish at .
Figure 5 is a picture of each of the first 7 steps and where we finished on the number line.
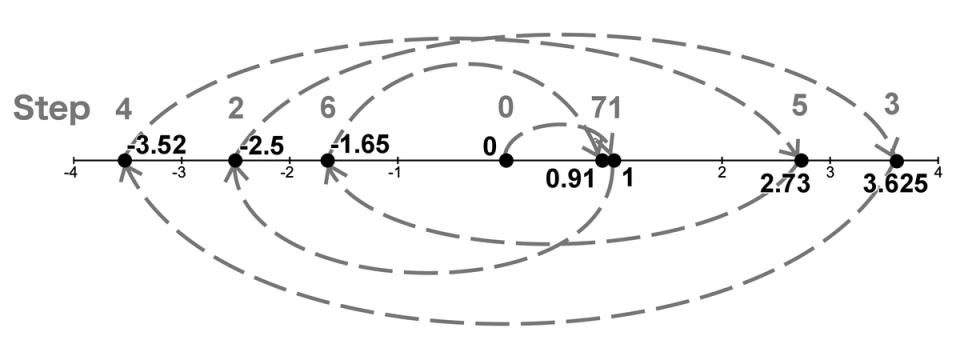
Figure 5. Straight -3.5 dance start
We certainly created a chaotic dance! What do you observe about our dance so far? Notice after every move we finish on a different side of the point 0. In other words, after an odd-numbered step, we finish to the right of 0. After an even-numbered step, we finish to the left of 0. Does this pattern continue forever? If so, then it seems like our landing point will be where we started, at 0. Go ahead, cast your vote. Do we finish at 0?
If we don’t finish at 0, do we finish to the left (negative number) or right (positive number) of 0? We solve this mystery once we perform the 12th step. Before going there, our instinct might tell us that the even number 12 means we expect to finish to the left of 0. If you’re up to it, you can perform the math. I will show you a picture of where we finish after each step. Let's zoom in our number line in Figure 6, so we can appreciate the finer details.
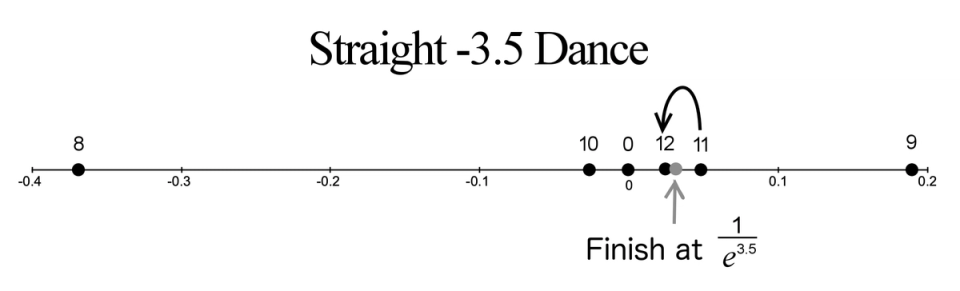
Figure 6. Straight -3.5 dance finish
After 11 steps, we are at the position 0.0488. Then, in our 12th step, we move a distance 0.0242 to the left where we remain on the right side of 0 and land at the positive position 0.0246. Notice we continue to zoom in at an ending point. The ending point is approximately 0.030197. The precise ending point is at , which is the same as .
In short, when we perform our Straight -3.5 dance, the total distance we travel remains . Another way to think about it is if we had a GPS system tracking our steps, it would indicate our distance traveled is . However, because we rotate directions after each move, we finish at a distance of only to the right of our starting point. If we want to write this in a formula, we can follow the familiar pattern we established for positive real numbers and now extend it to all real numbers:
So, for , we get:
Adding inputs, multiplying outputs
There are so many things to marvel at here. Observe when we let , we get . When we let , we get . Now, consider the combination of these two values for . We know if we let , our output is . Since , can we derive the output for by using the outputs for and ? In other words, when , our output is , and when , our output is . Can we combine and to get ? Recognize we must multiply by in order to generate the output for . Notice what just happened? We identified a rule, or a property, that when we add our inputs, , we can calculate our output by multiplying the outputs for each input.
As a result, this special dance we’ve generated has a unique property. Using this property, we can consider two different dances, say and , and derive the output for the sum of these two, , by multiplying the outputs when and . In short, let inputs be and . The outputs are and . Now, multiply the outputs, . Sum the inputs to get . The output is also .
If you review the recipe for our dance steps, this property of multiplying outputs when we add inputs is not obvious, at least not to me. Hopefully, we have enough familiarity with this dance that we can now introduce heavy math notation. If we label the two inputs as and , then we can define their output using the function symbols, and , respectively. Thus, we can write
=
Likewise, we can do the same for :
If we add our inputs, , we can write
And the result is no different from multiplying the initial two outputs:
There are two key points I’m trying to illustrate.
First, we need to understand the concept of adding inputs translates to multiplying outputs. Once we understand this concept, the second point is to ask why. Looking at the formula for , I am not able to identify any obvious clues that it will be the product of and .
Do you see any reason why the principle of “adding inputs equals multiplying outputs” works here?
Ruminating on e
Before we introduce new dance routines, let’s consider one more interesting idea that our dancing can highlight.
Recall we first introduced as the result when we start with money doubling every year and increase the compounding so it occurs continuously. We were able to write this in a formula: take the limit of as approaches infinity.
I find it interesting that math textbooks do not have a unified definition for . Unlike which enters the world through a circle and is clearly defined by comparing the distance across to the distance around, can be defined from several perspectives. To me, this highlights the many dimensions and perspectives has. Another way we can bring into the math world is to define it as the sum of our infinite series when .
Even though this is an infinite sum, this definition seems easier to grasp than the limit of . The limit of this expression as approaches infinity is a challenge because there are two ’s at play and they appear to be fighting for dominance. As increases, the term decreases, so the sum decreases and approaches 1. But raising any number greater than 1 to a large will increase the expression. It’s interesting that there is not a clear “winner.” Rather than having a clear winner, which would result in the limit approaching either 1 or infinity, the result is more of a compromise as it results in about 2.718.
Not only do we have the competing factors that make it difficult to estimate the limit, but the limit of only calculates . However, our infinite sum can calculate raised to any real number. Thus, not only can we calculate , we can calculate other values that don’t make as much sense to have as an exponent. We can think of as and that makes sense. But how do we interpret ? That number is difficult to interpret using repeated multiplication. However, when we view this as an infinite sum where is not an exponent, then all this makes sense.
Thus, if we want to enjoy the richness of all that has to offer, we should think of in terms of this infinite sum. Don’t forget that we arrived at this infinite sum by considering an infinite dance. To me, it is easy to picture taking steps forward according to our pattern simply by identifying each term in the sum. Remember the distance traveled in the th step is .
Considering a different dance
Wasn’t it fascinating when we considered dances for ? Yes, it was a bit dizzying because we performed a half turn after every step. However, it was enticing to anticipate where the dance finished.
Math friends, if making a turn after every step was exhilarating, do we dare ask what would result if we only made a turn after every step? In other words, let’s use the same distance formula we have been dancing with but make a turn to the left after every step.
If allowing a negative was not bold enough, notice the impact that a rotation creates. We must exit the land of a one-dimensional number line since our rotation will not be just a forward and backward motion. Before we perform this new dance, I encourage you to pause and envision what it will look like. Where will it go? Where will it end? Don’t worry, I’m confident you have the flexibility to dance with me as we veer away from the comfort of our number line.
One small rotation for math, one giant leap for mathkind
Our previous dance, which we labeled the Straight dance, was one-dimensional. Since rotating of a turn creates a two-dimensional dance, it seems appropriate to name our new dance “Rotate ” dance. Rotate dance is exactly the same as the Straight dance except we include a turn to the left after every step.
Because we’re rotating, we need more space to move, which means expanding our number line. The logical choice is to use our -coordinate system. Please take note that we are not required to use the -coordinate system. It’s just that we need another dimension and we already have the -coordinate system available, so there’s no need to reinvent the wheel (at least not yet).
Remember the distance for the move is . Therefore, the step of our Rotate dance is as follows:
Make sure you agree with me here since we will soon unleash this dance routine. Remember when we set for our Straight -3.5 dance, the total distance we traveled in our dance was the same total distance when . We just included a turn before each step. Thus, our Rotate dance shouldn’t feel much different from our Straight dance because we already know how to calculate the distance we travel. The distances we travel for the Rotate and Straight dances are the same for a given .
I’m a runner and I think about this in terms of running. For a positive , our Straight course was a point-to-point run. Then, when we let go negative, it was mostly an out-and-back repeated route. What type of route do we envision here? Because we’re rotating of a turn to the left, I envision it to be like running around the block. But, similar to how our out-and-back course never turned around at the same point, I envision our around-the-block course will also not follow the same block after completing 4 left turns. Some curious questions pop into my mind as we prepare for this dance. Will we ever cross our starting point? Will we end near our starting point? I do hope you are envisioning what this route may be and are curious to find out.
Rotate 1 details
Here’s the step-by-step story for our Rotate 1 dance. Our first move remains , which is always 1. Let’s assume we start each dance at the origin and our first move is in the positive direction of the -axis. This plan is consistent with our Straight dance where we started at 0 on the number line and moved to the right. We start at (0,0) then arrive at (1,0) after our first step. Then, rotate of a turn to our left. This points us in the positive direction of the -axis. The distance we travel is, which is 1 again. That means our second step is to move a distance 1 up from the point (1,0). Now we’ve arrived at the point (1,1). Again, take a turn which now faces the negative direction of the -axis. The distance is , which is . That leaves us resting at (, 1). Then, turn to the left and move down the distance , which is . Now we rest at (, ). Then, we turn to the left again and face the direction of the positive -axis which is the direction in which we began.
Our next distance is , which is , so we are at the point (, ). The next distance is , which is , so we are at the point (0.5417, 08417), since = 0.5417. All of these dance moves are illustrated in Figure 7.
Figure 7. Rotate 1 dance start
Do you see a pattern developing? We know this process continues forever and we don’t know exactly where we land, but can you identify from the plot that we are converging to a resting place?
What else do we know? We know the distance we traveled. Even though we took a left turn at every step, the distance traveled as recorded by our GPS system would indicate we traveled a distance . Of course, we are closer to the origin than the distance because of our turns. OK, math fans, where did we end after our infinite journey?
Before I answer, let’s make sure we’re clear on our perspectives. As I share several results from our Rotate dance moves in graphs, be sure to note the different perspectives. Sometimes I zoom in to see finer details and sometimes I zoom out to see a bigger picture. You can identify the detail and size of our landscape by noticing the distances on the -coordinate system. Remember these graphs are dynamic so you are free to zoom in and out of any graph you desire to see a perspective that is different from the default view.
Let’s take a super zoomed-in view to see the results after 8 steps. We finish at (0.5403, 0.8415), which is extremely close to our finish after 5 steps, as illustrated in Figure 8.
Figure 8. Rotate 1 dance finish
Even though this dance is interesting, the numbers we finish at are not. At least, they don’t appear interesting. But since I’m having so much fun, let’s try the Rotate 2 dance.
Rotate 2 details
Here is a quick tour of our Rotate 2 dance steps.
Start at , and move right to .
From , move up to .
From , move left to or .
From , move down to or .
From , move right to or .
From move up to or or .
From move left to or or .
From , move down to or or .
Where we finally finish our dance, to a more modest 3-decimal place accuracy, is (-0.416, 0.908). All the steps are documented in Figure 9.
Figure 9. Rotate 2 dance
We can identify that we are “circling" this ending point with the steps we’ve documented so far. Notice that even though we converge to a point, our step distances don’t always decrease from the distance of the previous step. Our first step is a distance 1, but our second step is a distance 2 to go from the point (1,0) to (1,2). Our third step is also a distance 2 to go from the point (1,2) to (-1,2). Then, our next step moves a distance of , which is , so we are decreasing our distance. Perhaps you understand why. To go from step to step , we take the distance from step and multiply it by . That means the factor we use to calculate the next distance is for step 1, for step 2, for step 3, etc. We multiply the numerator by 2 and multiply the denominator by the next larger integer. Thus, if we are doing our Rotate 2 dance, then we start decreasing the distance when we multiply the denominator by 3.
Let’s take a quick view of our two dances together. Figure 10 combines the Rotate 1 and Rotate 2 dances.
Figure 10. Rotate 1 and Rotate 2 dance
I included a dot for the ending point for both dances, but we don’t have enough detail to distinguish it from the step 8 point. What are your thoughts or observations?
Rotating patterns
Can you envision how this will play out for the Rotate 3 dance? In our Rotate 3 dance, we multiply the numerator by 3 each time while still using the same pattern for the denominator. That means our distance will start decreasing when . Do you envision a pattern where we travel around a bigger area but still settle down at some point? Let’s view the 8 steps for the Rotate 3 dance (red line) alongside the first 8 steps of Rotate 1 and Rotate 2 dances (gray dotted lines) in Figure 11.
Figure 11. Adding the Rotate 3 dance
Notice we’re not converging as quickly as we did with Rotate 1 and Rotate 2. However, we still appear to converge to the point that we are “circling,” so to speak, with straight lines. Because we travel more distance, the spacing for Rotate 3 allows us to distinguish the ending point after step 8 from other points on the graph.
Are you curious to view our Rotate 4 dance? Here are the first 8 steps of Rotate 4 (red line) next to the 8 steps of Rotate 3 (gray dotted line) for context. I zoomed out our graph in Figure 12 a bit to allow for a dance that covers more space.
Figure 12. Rotate 3 and Rotate 4 dances
After 8 steps, we have traveled a significant distance. But it appears we are near our ending point.
We have completed 4 rotating dances. Let’s pause and review where we finished after each dance. Is there a pattern to where we finish each dance? You can review Figure 13 that summarizes the exact ending point.
Figure 13. Ending positions for the Rotate dances
There appears to be some symmetry here. If we start at Rotate 1 and move to the ending point for the next dance, the ending point to the next dance appears to be about the same distance. In other words, the distance between the ending points for Rotate 1 and Rotate 2 appears to be about the same as the distance between the ending points for Rotate 3 and Rotate 4. Also, there appears to be a “rotation” of the ending points in a counterclockwise direction.
Certainly, one more data point may help identify any existing pattern. The next logical dance to review is Rotate 5. But rather than just extending our dance longer, let’s consider a dance that is in between one of the dances we’ve performed so far. So far, we’ve only considered integer values. But remember we used non-integer values for our Straight dance. For example, we looked at the Straight 3.5 dance and identified the distance traveled is . Rather than choosing a boring number like 3.5, is there a more interesting number we can consider that is also between 3 and 4?
Our dance with π
How about considering the dance Rotate ? I know seems like a strange input. However, aren’t you curious to see where we go and where we finish? We know the distance we travel with this dance because it is the same distance traveled in the Straight dance, which is . Of course, this appears to be a strange number because its base and its power both have an infinite number of decimals. Also, the two numbers are not related; is connected to a circle and is connected to exponential growth. Logic indicates the Rotate dance will land on some random obscure point in space. We can compute the distance traveled to, say 5 decimals, as 23.14069, clearly a random, uninteresting number. Let’s begin our dance and discover where we finish. We can follow the pattern from Rotate 2.
Start at (0,0) and move right / to (1,0).
Move up to (1,).
Move left to (,).
Move down to (,).
Move right to ( + ,).
Move up to (,).
Move left to (, ).
Move down to (, ).
Move up to (,).
After 9 steps, we arrive at the point (-0.976,-0.075). Let’s review our other points to see if this result meets a reasonability test. We would like to witness a pattern where the result for the Rotate dance is close to the result for Rotate 3 and in the direction of the result for our Rotate 4. Do you observe a pattern in Figure 14?
Figure 14. Rotate dance
This result does appear reasonable as we are close to the Rotate 3 ending point and in the direction of the Rotate 4 ending point. Also, the result appears to be purely random, which we would expect from mixing two different irrational numbers in an exponential process that seems to be random. To finish our math, let’s identify where Rotate finishes the dance. When all the moving and shaking finish at the ends of infinity, the final dance arrives at the exact point (0,1). Did you catch that? If not, you may want to reread the last couple of paragraphs because this is truly an amazing result of math. You can see this interesting result in Figure 15.
Figure 15. Ending point for the Rotate dances
I plotted the results for all the Rotate dances we’ve performed so far. Let’s review our Rotate dance, a dance that I think is worth writing about.
We start at the origin. We move a distance equal to in the th step. We try the unusual idea of letting . Notice everything we’re doing in this dance is about integers. We raise to the power , where is an integer. We use as the denominator. We start with , then we repeat the process for all positive integers. To add some rhythm to the dance, we make a left turn after every step. Bringing into this process certainly feels like fitting a round peg through a square hole. The number just doesn’t seem to belong. Though the total distance traveled, , looks interesting, it also seems random, like mixing oil and water. How would they ever combine into something meaningful? Yet, apparently, when we introduce the magic move of making a left turn after each step, a seemingly random dance results in us triumphantly landing at (-1,0).
The total distance we travel in our Rotate dance is . Now, think about what would be the distance we would travel if we start at the point (1,0) and walked along the unit circle until we get to the point (-1,0)? That distance is since this distance is halfway around a unit circle. We can easily calculate the scenic route we took on our dance steps if we start at the same point (1,0). The total distance if we start at the origin is . Thus, the distance traveled from (1,0) is . That means we have two interesting paths to go from (1,0) to (-1,0). We can follow the unit circle with distance . Or, we can perform our Rotate dance route and travel a distance of . Of course, if our goal is to go from (1,0) to (-1,0), the shortcut, but uninteresting route, is simply to follow the -axis with a distance of 2.
A circle of unity
Letting and landing at (-1,0) indicates there’s more to our pattern than just this one point. Let's review the ending points for our Rotate dances for . Can you connect the dots and uncover a pattern?
Let me connect the dots for all values from 0 to 2 . In other words, Figure 16 displays all the ending points for every dance between Rotate 0 and Rotate .
Figure 16. Ending point for all Rotate dances
Yes, the results for all our Rotate dances land on this circle. The radius for this circle is 1 and the center is at the origin. Also, there is a direct connection between the input for our Rotate 1 dance and where we finish on this circle. For example, our Rotate 1 dance landed at radian 1 on the circle, our Rotate 2 dance finished at radian 2 on the circle. If you’re not comfortable with the value for radian measures, 1 radian equals 180/ or about 57.3 degrees. Now, it should make sense why Rotate lands on the point because the distance halfway around a unit circle is .
Can we go beyond in our Rotate dance? Yes. For example, where do you think Rotate will finish? If the complete circle is , then if the pattern happens to repeat, we finish at the same point as - = . Recall our Rotate dance ended at , which is where Rotate is completed. However, it is a long dance. It required 25 steps to return near this point. Figure 17 shows the steps.
Figure 17. Rotate dance: beginning point , ending point
Notice how much we needed to zoom out for this dance as we wandered way away from our starting point at the origin. The total distance traveled is 12,392. Yet, we returned to the same circle with radius 1.
Isn’t it interesting what a rotation can create? What appears to be a random dance has an amazing ending at a precise point on this circle. We call this circle the unit circle or, as I referred to it before, the number circle. What we call it isn’t important.
You can say we have now gone “full circle.” Remember at the beginning of this section, we wanted our dance to end as a continuous flow even though we achieve the flow through discrete steps. We highlighted all of the steps and found regardless of what we used as input into this “dance,” we always finished on this nice continuous circle. So we certainly can go directly from our input to the point on the circle. But we want to remember that we traveled many steps to get there even if we lose focus of the precise steps we took.
Not only that but now that we know the Rotate dances finish on the unit circle, it is not so surprising that when we let , we finish at the point (-1,0). This is because we know plays nicely with circles. And not only does the dance finish on the unit circle, but the finish point (beginning from (1,0) on the circle) is exactly distance around the unit circle. We know the distance halfway around a unit circle is , so the logical result is we will finish halfway around the circle when we let .
We will dance more later in Lazarus Math, so keep your dancing shoes ready!










