“You must see math before you can do math” - me
Introduction
Because many math problems converge to a single answer, it is easy to perceive a polarization process of either you got the right answer or you didn’t. If you didn’t get the right answer, you get the feeling that math is not for you but for those who get the right answer. This creates this idea of “insiders” and “outsiders.” Those who don’t get the correct answer are “outside” and they view others as “inside.” This polarizes our view of who can do math. We all have the ability to think about abstract concepts in a logical way. Some people need more concrete examples to understand the concept. Needing to see concrete examples doesn’t make one a math outsider. It is just a different way of thinking.
I think the polarization results from too much emphasis on the final answer. Sure, arriving at a correct answer is a good thing, but there is so much more to math than the destination. We have already discussed the wonder that both geometry and algebra are consistent. That is an amazing thing. Both approaches follow logic and reasoning and finish at the same point. The key to your math coming alive is to believe you have the mental capacity to “succeed.” We “succeed” when we focus on the process.
Focusing on the process means understanding concepts. We understand concepts by viewing them from different perspectives until we find a perspective that “makes sense” to us. Then we need to practice to build that understanding with slightly different problems. This will make that understanding stronger because we see all the different nuances that can occur. Doing math this way is such a wonderful process. It is not recipe following. Rather, it is a growth process of understanding how things really work.
In this next section, we will emphasize the value of a different perspective. One that can make a difficult problem seem relatively easy because of a creative approach that I think many of us could have created if we gave the problem some time and space. Then we will test that understanding by applying it to slightly different examples so you can truly understand. No formula or recipe required!
We have reviewed several infinite series so far. Let’s consider a different infinite series.
Eating pizza
Consider the sum of this infinite series:
Notice each term is of the previous term. In other words, and , etc. Does this seem like an interesting series? How does this compare to the harmonic series? Both are an infinite series that involve positive integers. Recall the harmonic series has the positive integers resting in the denominator of a fraction. In this series, we are given a specific fraction, , and now the integers are resting as an exponent. It’s like we are taking the previous concept to a new level. But we are still working with basic ingredients—one fraction and the positive integers.
So our natural question is: What does this sum equal? Your immediate response may be that it trails off to infinity, similar to our harmonic series. However, in the previous dance moves, we summed an infinite number of positive terms and landed on a specific value. Will this infinite sum finish at a specific number?
To answer, let’s continue our playful mindset and pretend you have a pizza in the shape of a square. You may recall we used a round pizza when we calculated the area for a circle. We like pizza, and pizzas come in different shapes, so let’s stick to our carb-loading diet and order a square pizza.
Of course, eating the entire pizza by yourself is too much of a good thing, so you invite 2 friends and divide the pizza evenly among the 3 of you. How do you accomplish this goal to keep everyone happy and equally carb loaded?
You could try cutting the square by eyeballing a rectangle the size of a third of the square. But cutting a whole into 2 equal parts is easier than cutting it into 3 equal parts. We can use the vertical and horizontal lines of symmetry to cut the square into 4 equal parts and give each person a square piece. Perhaps you receive the teal piece and your friends receive the other 2 pieces. Since there are 3 people and 4 pieces, there will be one piece remaining as you can see in the top left diagram in Figure 1.
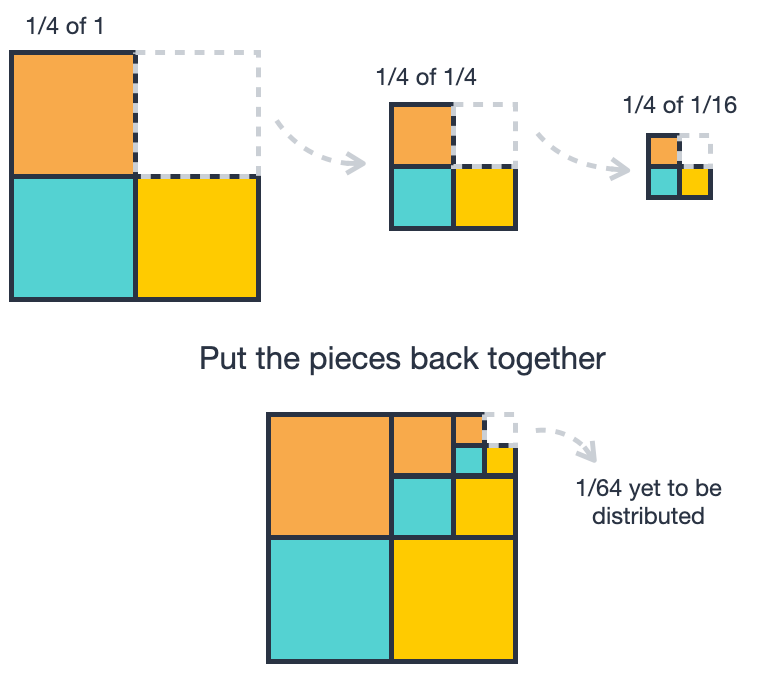
Figure 1. Splitting a square pizza
Then, take the remaining piece and cut it into fourths using the same strategy of using 2 cuts to create 4 equal pieces. Again, distribute 3 of these pieces to each person, so everyone receives 1 piece as you see in the top middle diagram of Figure 1. Still, 1 piece remains as shown in the top right diagram. Notice this is the only remaining piece and it is the size of the previous remaining pieces, so it seems like we’re getting closer to distributing the whole pizza.
We can repeat the process of cutting the remaining square into 4 equal squares, distributing 3 of the squares and leaving one. Observe the result of these first 3 steps in the diagram at the bottom of Figure 1 which puts the pieces together. Each time, you receive the teal piece and your two friends receive one piece each, leaving one square that needs to be distributed. That encourages us to repeat the process: cut the remaining piece into 4 pieces, give one piece to each person, and have one piece remaining that is the size of the previous remaining piece.
In the real world, this process would end because the remaining piece eventually would be too small to cut. In our abstract math world, we can let this cutting and dividing process trail into infinity. That means we can continue this process until the piece that needs to be distributed approaches 0 in size. The question we’re wrestling with is: When we allow this infinite process of cutting and distributing to continue forever, how much of the pizza did you receive? In other words, what part of the whole is the sum of the teal squares?
1/3 (the fast way)
There are at least two different ways to view this. The easy and fast way is to realize there are 3 people and everyone received the same amount. Since we allowed the cutting and distributing to continue until the missing piece approached zero, the entire pizza was distributed. Thus, by definition, there is no leftover piece. Since the entire pizza was evenly distributed to 3 people, then you and your two friends each received of the pizza. Would you agree? What could be simpler? It's just you and two buddies equally dividing a pizza. Everyone gets the same number of equally sized pieces, which means each of you received of the pizza. Wasn’t that clever?
Rather than digging into the details of the math, we can observe the big picture where every person receives the same amount of pizza after every distribution. Thus, in the end, everyone has an equal share of the pizza, and since we divided a whole into 3 equal parts, each person received of the pizza. Isn’t it interesting that we solved an infinite sum without doing any addition in the process? We didn’t even need a formula. We can see the answer by viewing the big picture of the process from beginning to end. Also, isn’t it interesting that we can see how an infinite sum equals an exact number? It couldn’t be less than because then it wouldn’t be completely distributed, and it couldn’t be more than because the sum can’t exceed the whole. It must be exactly .
1/3 (the slow way)
We identified the fast way to solve the problem. What is the slower way to quantify the fraction of pizza you received? The second way is to review each of your pieces, calculate how much of the whole pizza each piece represents, and sum each fraction. How much did you receive with your first piece? Remember the first cut divided the pizza into fourths, and you received 1 of 4 pieces, so your first and largest piece represents of the pizza.
Assume you receive the lower left corner piece (teal color). What does your next largest piece represent? Now, assume the piece that was not distributed in the diagram (Figure 1) is the white piece in the upper right corner. Your second piece started as , then it was divided into fourths again. The size of your second piece, therefore, would be a fourth of a fourth, or . Again, assume you get the piece in the lower left corner. Next, let's consider your third piece. How much of the whole pizza is it? Again, the piece that is not distributed is the white piece. This white piece started as and was divided into fourths, so it is of or , which is .
Remember, in the real world, we stop this process when the remaining piece is too small to cut. But, in the math world, there is no such thing as a number too small to divide. Living in the abstract world allows us to continue this process forever. Then, when we add all the pieces together, notice we produce the original sum we were asking about. That means we created this amazing formula:
Sum =
Here is a graph of the sum where each step up, going from left to right, represents the amount added for the next term. Thus, using one term, the sum is . Using two terms, the sum is , or . The sum using three terms is , which we can identify from Figure 2.
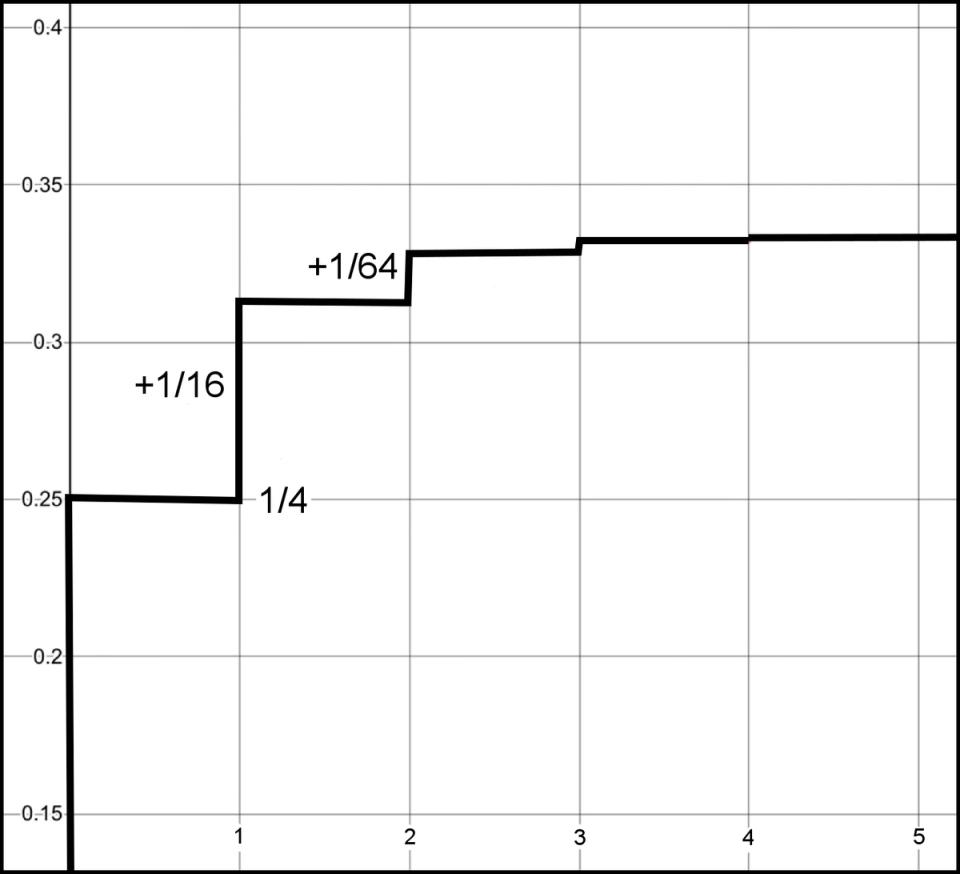
Figure 2. Reaching 1/3
The sum of this infinite series is . Exactly.
From this picture and process, perhaps you can see why. If you can follow this story, you can “do math.” It’s not about manipulating equations. It’s about changing your perspective on the problem and viewing it in a different light. Here, we just had to imagine a simple process of slicing and distributing pizza with our friends, then recognize the abstract concept of sharing fourths and fourths of fourths, and just repeat this process.
1/3 (the finite version)
Good work! We found the beautiful result when we let this process continue forever. It equals exactly because we learned how to divide a pizza evenly by cutting it into fourths.
Let’s continue using a pizza because, as we know, pizza and math pair well together. You’re getting the hang of it, so let’s imagine another square pizza. But think of a really huge square pizza, one that we can divide between 3 families. We’re making the pizza super large because we want to perform this process 6 times. Remember the process: cut the pizza into , then distribute 3 of the pieces. That means after 6 rounds of slicing, we would have this sum:
Assuming you are one of the families that receives this pizza, how much of the pizza have you received so far? We could calculate this sum, but that would be messing with tedious details. Adding numbers like this is what we want computers and calculators to do. What we want to do is play and find patterns or, as some call it, use shortcuts. Some shortcuts shorten the process but reduce understanding. Because this shortcut simplifies and increases understanding, I refer to it as a beauty cut.
A beauty cut
What we want is something eloquent, something special. How can we look at this problem in a different way? We already identified that if we didn’t stop this process, the answer is . Rather than computing what you have, can we start with the remaining piece and imagine how much more you would receive? Because we know you would receive in total if we never stop, then if we can quantify how much more you would receive after the 6th cut, we can subtract that amount from to get how much you’ve received so far. I’ll write it in math terms to be more concise.
In other words, assume there are 25 marbles in a jar and I remove an unknown marbles out. One way to identify is to count the marbles I removed. But if I notice there are only 3 marbles remaining, then I can deduce that I removed 22 marbles since . We give this strategy a fancy name—complement strategy. If you know the total and you split the total into two parts, you only need to calculate one part to get the other part. We perform this “trick” often when calculating probabilities. Here is a simple example to illustrate the complement strategy.
Snake eyes is when you roll two 1’s with two dice. Since there are 6 sides to the die, what is the probability you do not roll snake eyes? It’s much easier to calculate the probability you do roll snake eyes, which is , or . That means the probability you do not roll snake eyes is the complement since we know the probability for all possible rolls is 100% or 1. We also used the complement strategy earlier in the book. Remember we labeled the Euler-Mascheroni constant as . Then, when we wanted to calculate , we identified it was the complement to , i.e., . We have the same concept here where we apply the complement strategy.
The complement strategy
How much do you receive after 6 cuts? All we need to know is how much the remaining piece is relative to the whole. The last piece was . That means the remaining piece is also . How much of that piece will you receive? By definition, we know that this piece will be divided equally among 3 families. Thus, you will get of of that last piece. That means the sum after 6 cuts that you will receive is .
As a result, we can calculate the amount you received after 6 cuts as or , only a little less than , which we expected. Pretty slick? Notice one shortcut (or beauty cut) we took here was we quickly calculated the remaining amount as of because we knew that piece would be equally divided among 3 families. However, we could have written the size of each remaining piece. Notice the size of the first piece is of . Then, the next piece is of that or x . Of course, this process continues forever. Thus, if we wanted to write some messy math, we could write:
Notice how similar this is to our original problem except we have an extra factor in every term. But isn’t that what was going on? Both the original problem and the second problem where we start with a smaller piece were performing the same operation. Both examples continued forever. The only difference was the second process started with a piece that was of the whole. Thus, it should make sense that we can just use our original formula and multiply by .
This concept may be easier to see by reviewing Figure 1. Notice after each step, we start with a square and then repeat that same process forever. So, if we gave away our first piece in Figure 1, we can begin with the second step and recognize we eventually receive of the second square, which is of the pizza. Thus, in total, after the first step, we receive of the pizza. The reason is that we can “start” at any part in this process because we always have a square that needs to be distributed. Each time, we divide a square into 4 pieces and always have one square that is not distributed, which begins the process again. Thus, if we start after 1 iteration, we just need to understand the square we are starting with is of the whole, so we just multiply the end result of by .
This illustrates a common theme in math that is counterintuitive. When working with an infinite number of terms, often it is easier to calculate the sum of an infinite number of terms than it is to calculate the sum of a finite number of terms. Notice we always receive of the part we start with, whatever that part is.
We have performed quite a bit of math. Let's summarize so we do not get lost in the details. There are two main concepts to grasp.
First, we have a process of cutting into fourths and distributing 3 of the pieces which leaves one piece to cut and redistribute. We perform this operation an infinite amount of times and realize that we eventually receive of the total. This process of assuming the cutting and dividing continues to infinity actually makes the math easier. This is truly an amazing concept because of how simple, yet profound, it is. So we tested this understanding by considering what occurs if we start at a different place in the process. Thus, we considered how much pizza we received if we started distributing a fraction of the whole, which leads to our second concept.
Second, if we want to identify how much we receive after a finite number of cuts, it may be easier to use the complement strategy and identify how much of the pizza has not been distributed. Then we can identify how much was distributed after a finite number of cuts as the difference. We were able to use the complement strategy because after every step, we began with another square to cut, divide, and distribute, and this square has the same properties as the original square, only smaller.
Conclusion
Perhaps you are skeptical and haven’t bought into this idea that an infinite sum can actually equal anything that is exact. Let me ask this: What is ? I think we all agree this is 1. It must be, right? OK, what is in decimal format? We know is 0.3333 with the 3’s flying off forever. Thus, when we add these 3 simple fractions, we’re adding 3 numbers that have decimals that continue forever. If we remain in the finite world, it doesn’t arrive at the number 1. The result will be 0.9999 with as many finite number of 9’s as you want to include. How do we get “over the hump” and arrive at 1? That is where the limit does its job. We assume the number of digits approaches infinity. When we apply this limit, the result settles at exactly 1.
This process happens to me a lot in math. At first, a concept new to me may surprise me, or not be intuitive. I hear of a concept like a limit for the first time, and it seems incredible. No way; I mean who is dreaming this stuff up? But after I play with it and see different perspectives, my brain slowly “gets on board” with what most of the rest of the math world is already at. This has happened so many times that now I look forward to a counterintuitive result and am not surprised when it occurs. For me, playing with math is full of surprises.
There is much more beauty yet to behold. In our next story, we will continue with the infinite sum process we discussed here. But again, we will view the sum from a different perspective.










