“It is through science that we prove, but through intuition that we discover.” Henri Poincaré
End of the story?
After I presented my field goal problem and its solution to my math club, the professors smiled and asked a few simple questions. The bar was set low, so I was in. You may think of this as the end of the story since we solved the problem. I sure thought it was the end as I accomplished my goal of joining a math club. Then, over 30 years later, I remembered some of the adult math moments from this story, so I decided to revisit this problem. Little did I know that this story would take on a whole new life and that there were more chapters to write.
It was a Saturday in February and, because I live in Iowa, the weather was nasty. The previous year or so, I’d read a lot about the history of calculus, so calculus was on my mind. I remembered this football problem, and it intrigued me again. Unfortunately, or maybe fortunately, I had thrown away my original papers. Being the curious type, I wondered if I could still solve this problem. It’s kind of like wondering if you can still fit into the pair of jeans you wore in college (which I couldn’t). I used calculus as far as needed for the actuarial exams but was pretty rusty on everything else. However, I was ready for the challenge, so I tried to recreate this problem and see if I could solve it. I don’t have perfect memory of how I solved the problem in college, but I think I solved it as I did in the previous section. It was surprising how much I did remember after all these years. That Saturday, I successfully calculated the same result: 17.73 feet away is the optimal distance for a college football field. Again, mission accomplished and end of story.
The next Saturday … beyond college football
Then, the next Saturday, another cold winter day, I was inspired by the satisfaction of solving the college football problem that I thought about solving the problem for a high school field. My first instinct was to use the high school field measurements and solve for that specific solution. Then I thought a more efficient strategy was to use variables rather than constants, so I could get a solution in terms of the variables and substitute any variables I want. This way, it would be quick to calculate the result for a pro field, for example. I wasn’t trying to accomplish anything or gain any new insights. I was just trying to be efficient. Let’s return to our work from the previous section.
We’re still assuming “Field Goal Position,” but now let’s generalize the terminology so we can apply the solution to a field other than a college-sized field. We already have most of the work done, with as the distance from the far field goal post to the hash mark, rather than the constant 29.5, and as the distance from the closer field goal post to the hash mark, rather than 18.5. As a result, our new problem is to solve for in terms of and . As a review, here is the general setup in Figure 1.
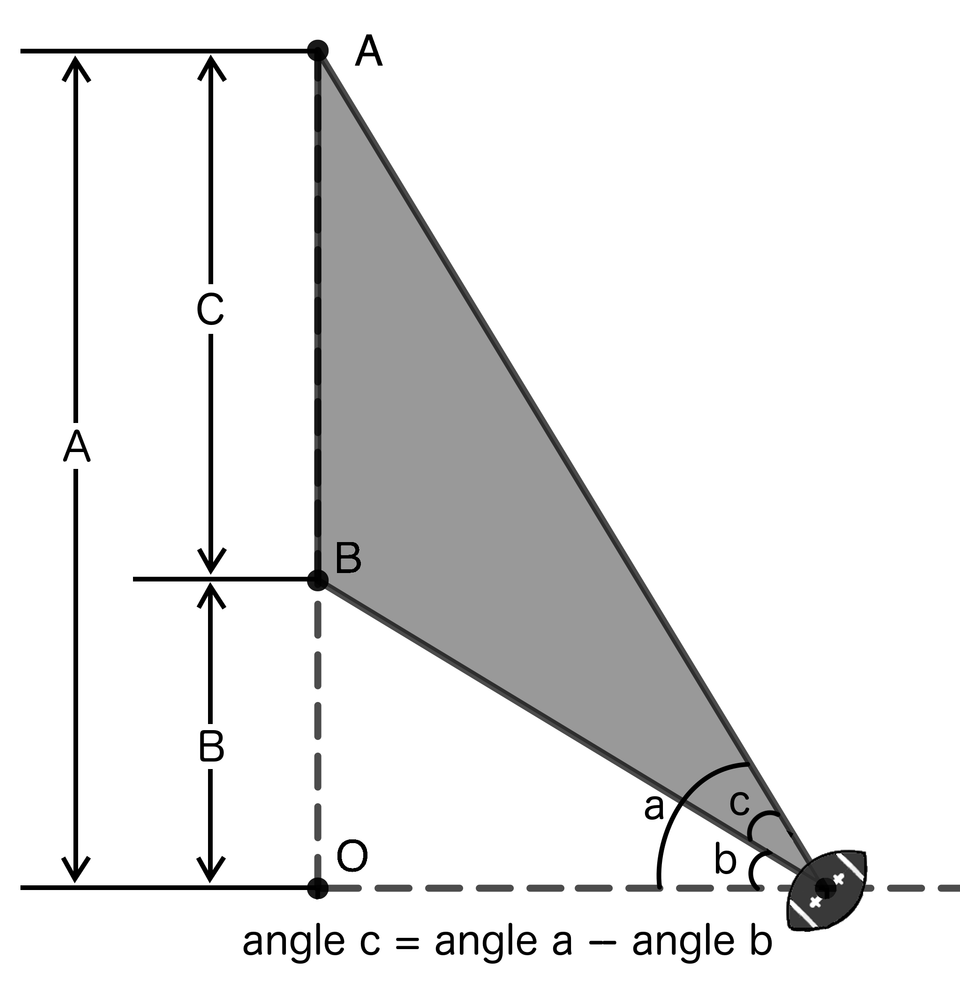
Figure 1. Refreshing our field goal position
Give me any football field
Because we performed so much messy math to get here, I was expecting the solution for to be a messy result in terms of and . Assuming you read the story, my hunch is you would have a similar expectation. That would be ok because it would allow me to substitute any field size for and . Actually, I was using a spreadsheet, so messy math was not a problem. Let’s see how messy our solution is.
Instead of starting at the beginning, we can simplify our work by starting where we converted and to numbers. We had part of this equation where the left side was a numerator of a fraction must equal 0. That means the numerator must equal 0, which produced this equation.
Starting here was quite encouraging because it was a relatively simple algebra statement with one unknown . Solving for is straightforward. Simply substitute for 29.25 and for 10.75 to create this expression.
From messy to beautiful
Because we are solving for , put the terms that include on one side.
Get by itself by factoring out the term.
Observe we have on one side and on the other side, which are the same multiplicative factor that we can divide out. In the end,
which means,
Yes, this did simplify to a simple solution. But this is much more than just a short answer.
Take a moment and think about what this result is stating. To appreciate the statement, we need context. Fortunately, the context is the previous story where we began with a simple question about calculating the best angle for a field goal. You know all the messy calculus and algebra we performed to get our answer. It was a journey through angles, triangles, inverse tangent functions, the difference of inverse tangent functions, and, finally, a derivative equation for the difference of inverse tangent functions.
If our goal was to simply solve for the field goal problem, what this is saying is we could have jumped right to this answer. Simply measure distances and , multiply, and take the square root. That is it. Are you kidding me? I had probably invested 50 to 100 hours on this problem, yet I stumbled into this solution that would yield an answer in less than a minute.
Rather than thinking I had wasted all this time, I was fascinated that something so complicated can be solved so easily. I already knew I gained a lot of benefits from my journey through the problem. Now I had a different question. My previous question was how to solve a seemingly difficult, if not impossible, question. My new question is: why does this difficult problem simplify to something as easy as this?
I was totally shocked that the result simplifies to something this beautiful and simple. By the way, the technical term for is the geometric mean of and . Of course, I just had to test this out to see if it was consistent with our previous result.
This reproduced our previous result, so it confirmed the solution is correct.
Another beautiful story
Before investigating why the solution is so simple, I thought of other seemingly simple solutions. To me, this is similar to the solution given by the Pythagorean Theorem. The Pythagorean Theorem states that no matter what the lengths of the sides of two right triangles are, the length of the hypotenuse always simplifies to the square root of the sum of the squares of the sides. In other words, if the length of one side of a right triangle is 3 and the length of another side is 4, then the length of the hypotenuse is .
After doing this field goal problem, I had a new appreciation for how remarkable the Pythagorean Theorem is. My natural thought was to wonder why the answer to the field goal problem was the geometric mean. What a beautiful answer! But WHY was it true?
Have you ever wondered why the Pythagorean Theorem is so simple and eloquent? Have you ever wondered why for any right triangle with side lengths and , the length of the hypotenuse is always ?
Would Pythagoras be happy?
Since I view our story and the Pythagorean Theorem as similar stories, let’s take a quick detour from the field goal problem and review a simple proof of the Pythagorean Theorem. As amazing as this proof is, it relies on intuition. To start, consider the triangle we just mentioned, a triangle with sides 3 and 4 and hypotenuse 5.
First, draw the side with length 3 on the vertical axis and length 4 on the horizontal. If we make a copy of this triangle and flip it, then we have a rectangle. What is the area of the rectangle? The area of the rectangle is , which is 12. That means the area of the original triangle is , as illustrated in Figure 2.

Figure 2. Two triangles with the same size and shape
Observe when we flipped sides, we also flipped the angles. If we use degrees, the sum of the angles for a triangle is 180. Since we have right triangles, then the sum of the other two angles is 180-90=90. We don’t know the individual angles, but we know that they are complementary, or that the sum of the two angles is 90. That means when we rotated our triangle, we created another right angle because the sum of complementary angles is 90.
You may wonder why we are calculating the area of a triangle, which is 2-dimensional, when we are only trying to calculate the length of the hypotenuse, which is 1-dimensional. You have seen this trick before when we reviewed the Madhava-Leibniz series in the Expanse portion of Lazarus Math. Because the math for area is consistent with the math for adding and subtracting numbers, we used techniques for calculating an area to solve an algebra problem. We are employing a similar strategy here.
Now, rather than placing the second triangle to form a rectangle, give this triangle a little nudge by rotating it of a turn in the counterclockwise direction. Notice in Figure 3, this forms a straight line of the two sides of a triangle. The length of the bottom triangle is 3 and the length of the top triangle is 4, so the total height of the two triangles is 7. Again, we know the combined area for these two triangles remains .

Figure 3. Moving the second triangle
Math is often easier when we have symmetry. We don’t have symmetry yet, but how can we modify this picture and arrive at symmetry? One way is to create a copy of these two triangles and flip the copies as seen in Figure 4. Of course, all 4 triangles have the same measurements, with one side equal to 3 and the other side equal to 4.

Figure 4. Triangles the same size and shape
Notice the symmetry we just created with our 4 triangles in Figure 4. Consider the shape of the outer shape we created. It clearly has 4 sides. The length of each side is , or 7. Since all four sides are the same length, and each corner is a right angle, we created a square of length 7. What is the area of this square? The area of a square is the length of a side times itself, or . What is the area of all four triangles combined in Figure 5?

Figure 5. Calculating the area for the inscribed square
Remember when we had only two triangles, the area was . Now that we have 4 triangles of the same measurements, their total area is . We have identified that the outer square has a total area of 49 and the shaded region has a total area of 24. That means the area of the unshaded region is the difference .
How else could we calculate this area? Notice the unshaded region also has 4 sides. Do we know the length of each side? We currently don’t know the numerical length, but we know it is the length of the hypotenuse of the triangle. If we let the hypotenuse length be , then the length of each side is . We would like to think that this unshaded region is a square with length , but we can’t assume that it is. However, we can easily prove it.
A proof
If we examine one corner of the unshaded region, the total angle it forms with the triangles on each side, we have a straight line that has a total of 180 degrees. Since the two angles of the triangles are complementary, the angle of the unshaded region is .
Because of symmetry, we have this same scenario for all 4 angles. If all 4 angles are 90 degrees and all sides have equal length, then the inner shape is indeed a square. Thus, the area of the inner square is . We know the area must equal 25. Therefore, or .
What is important here is not that we calculated the length of the hypotenuse for this one triangle. What is important is how we can generalize this for any triangle. Let represent the length of one side of the triangle, rather than 3 in our example, and let represent the length of the other side of the triangle, rather than 4. Using these definitions, what is the area of the outer square in Figure 6? It is . What is the area of the shaded triangles inside this square? The total area is two times the product of each side, or .

Figure 6. Connecting A and B to C
Then, what is the area of the inner square, where each side is a hypotenuse? It is the difference between the area of the outer square and the area of the shaded triangles, which is . But if the hypotenuse is length , then we also know the area of the inner square is . Thus, we just proved the Pythagorean theorem that .
Remarkable
This is an eloquent crystal-clear proof of the Pythagorean Theorem. As far as math proofs go, this one is an all-time classic. It has been appreciated by math people all over the world for centuries. This is not only beautiful but also remarkable.
If you think about it, the proof is simply a story about shapes. It has been told to thousands of people from many cultures for literally thousands of years. The remarkable thing is we all believe it is true. How many stories can generate that much agreement? It certainly isn’t intuitively true. We simply used a few basic shapes, moved them around a bit in a way that was symmetrical, and asked the right questions. The answers were fairly straightforward.
Isn’t it amazing that we can all arrive at the same conclusion? Triangles are similar to circles. They have a simple shape, simple definition, and simple structure. Yet, they have amazing properties once we take time to think about them.
A team on a mission
I shared this proof because I was wondering if there is a similar explanation for our field goal solution. My hope was that because both the Pythagorean Theorem and our field goal problem simplified to an eloquent solution, there would be a simple explanation why the solution to the field goal problem is the geometric mean.
To answer that question, I had to understand the root issue here. As we’ve discussed, this problem is all about triangles, which are straight lines. The answer to this problem is the geometric mean, which is the average of a curved line, an exponential line. The question gnawing at me is why a problem involving triangles has a solution that is an average of an exponential curve. An exponential curve is about multiplication. That means there is multiplication hidden in this problem. But where? Sure, we sketched a curve for angle . But why is there an exponential connection between and ?
Thus, I set out on a journey to learn why. I spent weeks thinking about this and even recruited some of the bright young actuaries at our company to answer this question. Could this team uncover the reason WHY?
Similar triangles to the rescue
As our small team was eating supper and brainstorming using whiteboards, one idea surfaced. We remembered the property of similar triangles from basic geometry. The idea is to start with one triangle, modify the length of each side by a given constant, say , then create the same shape of the triangle with these new sides. It’s like shrinking or expanding a triangle without changing its shape, just its size.
We didn’t know if this was important, but it is an interesting property of triangles, so we decided to see what happens if we change the size of our triangle but not the shape. Thus, we started with our triangle in “Field Goal Position.” Then, we wondered what would result if we had a triangle half this size. Again, we didn’t know if this was important, but we were just investigating a hunch.
We have two right triangles sharing the same side with length . We can create similar triangles that are half the size by using the right half of these triangles and setting the new length as where is half the length of . Now, we have a new left side for both triangles.
Let’s use a different notation for our smaller triangle. Use and to replace the corresponding and in the larger triangles.
Since our new triangle is half the size of the original, then and . Because we only changed the size but not the shape, this is similar to the setup we had before. In other words, we can view the smaller triangles as a new, but similar, field goal problem. The only change is we have different goal post distances. We can consider this smaller triangle now as the new "Field Goal Position.”
Given this new setup, how did our angles change? Observe in Figure 7 that the angles don’t change when we change the lengths of the sides by the same constant. This is the property of similar triangles.

Figure 7. Field goal problem preserved with similar triangles
We can also prove the angle measurements are preserved. Clearly, angles and did not change. The -axis and the new vertical side remain perpendicular to each other, so the angle between them is a right angle, consistent with the right angle from the larger triangles. That means the third angle for our triangles must remain the same. If the measurement for two angles of a triangle do not change, then the third angle does not change since the sum of the angles must always equal 180.
With this setup of smaller similar triangles in place, we can ask if is the geometric mean of and . In other words, does ? If this is true, we know this new is the correct distance to maximize angle , given the smaller triangle in our new “Field Goal Position.” Let’s investigate this question.
Searching for a multiplicative process
We know that , but we don’t know if is the geometric mean for the new and . Since , then . We can rewrite 2 as . .
Next, rearrange as . Since and , we conclude that .
This shows that if we multiply the sides of the original triangle by , then the solution to our football problem is the original divided by 2.
Of course, if we multiply by a different constant, then the solution to that field goal problem is times this constant. The answer is yes, the field goal problem is preserved by multiplication because of the property of similar triangles. Notice what is hidden in the property of similar triangles is a multiplicative process.
If we think of a graph of an additive process, we think of a line. But, if we think of a graph of a multiplicative process, then we have an exponential growth and we think of a curve. That means hidden inside the 3 flat sides of a triangle is a multiplicative process that involves curves. One more interesting feature of triangles!
But there are a lot of curves and multiplicative processes. Why does our solution reduce to essentially the simplest solution possible, the geometric mean? The geometric mean is simply the average of two numbers using multiplication.
We’re used to seeing the average of two numbers using addition. Notice we get the average of and using addition by adding the two numbers and, using the next higher operation, which is multiplication, we multiply the sum by 1/2. Likewise, we get the average of and using multiplication by multiplying the two numbers and, using the next higher operation, which is exponentiation, we raise the product to the power 1/2 by taking the square root. Thus, . So, why is this multiplication average hidden in our field goal problem?
But why the geometric mean?
Where does that leave our story? After several weeks, our creative team became satisfied that we have a multiplicative process going on based on how the problem is preserved using similar triangles. However, despite all of our brainstorming ideas, we were never able to understand WHY the solution simplifies to the geometric mean. This story appeared to have another ending as we were out of ideas. I was ready to consider this a question that won’t get answered. Not every mystery is solved.
It took a seemingly random meeting with a new math friend to nudge me in the direction to the clue I needed. Ironically, the clue I needed was based on a circle. The next story is about a circle and its surprising solution.















