Geometric Sum

“The flaw in the Greeks’ logic was the assumption that you can’t add up an infinite number of things and get a finite answer. Calculus showed that you can.” K.C. Cole

Multiplication magic

The focus for Lazarus Math has been to unleash the flexibility and opportunity for ideas we have in math. What usually challenges this notion is focusing on formulas. Of course, formulas are good, but the emphasis on formulas focuses on the destination and can shortchange the entire journey. In this section, I’m going to “buck the trend” a bit by taking the journey we experienced in the previous section and focusing on the destination. In the previous section, we considered an infinite sum by thinking of it in terms of cutting and dividing a pizza. Hopefully, that journey was enlightening.

Even though the formula is a “destination,” hopefully it will have more meaning since we gave the context of the journey to get there. We still have a little “journey” work to do before we arrive at the destination of a formula.

First, we need to identify the pattern within the problem. We see the pattern when we compare two consecutive terms. In our pizza example, notice the second term is always $\frac{1}{4}$ of the first term. This is a multiplicative pattern because we find the next term by multiplying the previous term by $\frac{1}{4}$ or 0.25. We call this a geometric series. So the key concept at play in this infinite series is we have a multiplicative process. When we have a multiplicative process, math magic happens. It is magic because this math works for other fractions, such as $\frac{1}{5}$ or $\frac{2}{3}$ or $\frac{1}{2}$, not just $\frac{1}{4}$. For this particular series, the magic only works if the fraction is larger than -1 and smaller than 1.

The series for $\frac{1}{2}$ would simply be $\frac{1}{2} + (\frac{1}{2})^2 + (\frac{1}{2})^3 + (\frac{1}{2})^4 + ...$. The pattern is simply taking the previous term and multiplying it by $\frac{1}{2}$. We refer to this factor $\frac{1}{2}$ as the common ratio. Identifying the pattern is important because we see how things get repeated. Like all patterns, where we end up depends on where we start. You and I may start a “pattern” by running 2 miles a day. If you begin as a world class runner and I begin as an overweight grandfather, our journey and destination will be different. Simply put, the last remaining piece to understand this infinite series is to identify the first term of the series. In the previous example, the first term is $\frac{1}{2}$. In this example, the first term and common ratio are the same $\frac{1}{2}$, but that is not required.

Now, we are ready for the formula that calculates the sum for this infinite series. The formula is quite eloquent. In words, the sum equals the first term divided by (1 minus the common ratio). In our example, the sum is $\frac{1}{2} / (1-\frac{1}{2}) = \frac{1}{2} / \frac{1}{2} = 1$. Again, in order for this formula to work, the common ratio must be greater than -1 and less than 1.

Pizza—all mine

Actually, I think you could have identified the sum of this infinite series before you read the book if you would have thought about it in the right perspective. Again, it is about cutting the pizza evenly and distributing the pieces. This time, assume the pizza is in the shape of a circle. We’ll assume I am the one eating the pizza but feel free to join me. The difference in this example is the pizza cutter is me, and I am eating the pizza alone, just me and the pizza.

I want to exercise portion control, so I decide $\frac{1}{2}$ of the pizza is a good portion. Since I am the only one eating, I cut the entire pizza in half. I eat one piece, which means one piece that is size $\frac{1}{2}$ remains. My original plan was to eat only $\frac{1}{2}$ of the pizza. But, now that I have eaten it and I smell the other half in front of me, I think I should eat more. You probably know how this story ends.

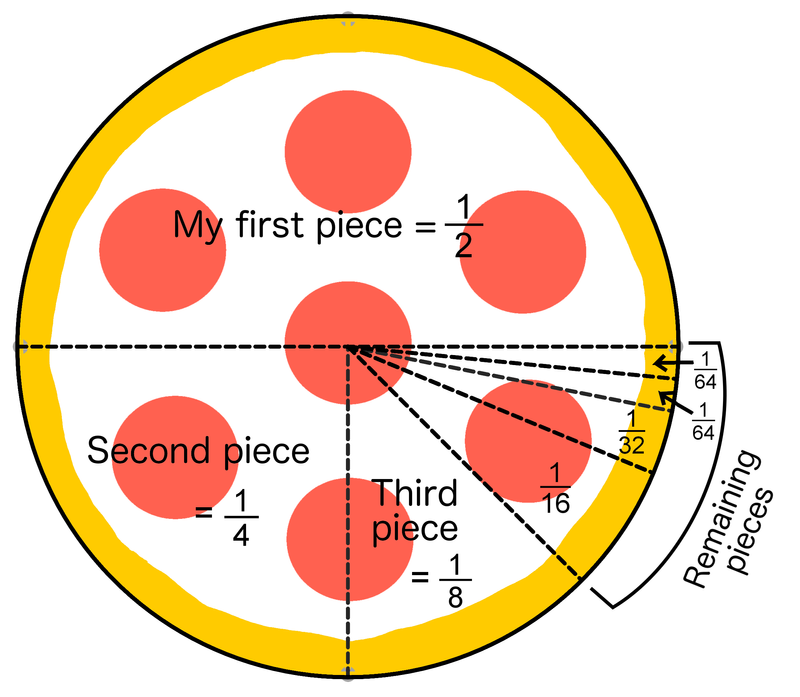
I’m not going to just eat the other half of the pizza. No, again I attempt to exercise portion control. I cut the remaining piece into two halves again with the plan of only eating one of the pieces. So, I eat a second piece, which is $\frac{1}{2}$ the size of the first piece. Now, let’s evaluate how much of the pizza I have eaten. I have eaten $\frac{1}{2} + \frac{1}{2}$ x $\frac{1}{2}$ or $\frac{3}{4}$ of the pizza so far. Or I could use the complement strategy and determine how much I have eaten by identifying how much remains. The size of the pizza that remains is $\frac{1}{2}$ x $\frac{1}{2}$ or $\frac{1}{4}$. This indicates I have eaten $1 - \frac{1}{4}$, or $\frac{3}{4}$ of the pizza.

One would think eating $\frac{3}{4}$ of a pizza is enough. However, the remaining $\frac{1}{4}$ of a piece still looks and smells good, so I cut the remaining piece in half and eat one of the pieces. The size of this piece is $\frac{1}{2}$ of $\frac{1}{4}$, or $\frac{1}{8}$. That means $\frac{1}{8}$ of the pizza remains. How does this story end? In the math world, it doesn’t because I continue to cut the remaining pizza in half and eat one of the pieces and then repeat for the remaining piece. This produces an infinite sum:

After the process is completed as we approach infinity, I have eaten the entire pizza, so the sum must equal 1.

Eating leftover pizza

We can view this process a bit differently. Rather than starting with an entire pizza, assume I start with only $\frac{1}{4}$ of a pizza. Perhaps it is leftover pizza. But I follow the same process. Rather than going through the story piece by piece of me eating and cutting, let’s apply our formula.

What is the first term? The first term is the size of the first piece I eat. If we start with $\frac{1}{4}$ of a pizza, then after one cut there are two pieces that are each $\frac{1}{8}$ of the original pizza. Thus, the first term is $\frac{1}{4}$ x $\frac{1}{2}$ = $\frac{1}{8}$.

What is the common ratio? The common ratio is the same as before: $\frac{1}{2}$. In other words, I always cut the remaining piece in half. That means the infinite sum starting with $\frac{1}{4}$ of a pizza is:

Now, apply the formula by letting the first term be equal to 1/8 and the common ratio equal to $\frac{1}{2}$.

This matches what we expect.

The complement pizza

For fun, try this one. Let’s return to the story where I start with an entire pizza. However, this time we will assume I exercise portion control and it took 10 cuts before I was able to stop. Our question is: after I have made 10 cuts to the pizza and ate one piece of each cut, how much of the pizza have I eaten? We can write this out in formula:

Sure, we could add these fractions, but is there a better way? Can we use our formula? We can’t use the formula in its current form because the sum stops after 10 terms and our formula is for an infinite sum.

How can we solve this? Think about the complement strategy. We just identified if we didn’t stop, the sum equals 1. That means rather than solving directly for how much I have eaten, we can get to the answer by identifying how much of the pizza remains. Here is our complement strategy formula:

Amount eaten after 10 cuts = original pizza - amount of pizza that remains after 10 cuts.

The amount of pizza we started with was the entire pizza, or 1. How much of the pizza remains after 10 cuts? Our last remaining piece equals the last piece we received, which is $(\frac{1}{2})^{10}$. But if we follow the same process with this little piece, we know eventually I will eat it all. Thus, what I have eaten so far is 1 minus the total I would eat if I started again, which is $(\frac{1}{2})^{10}$. Therefore, the amount I have eaten thus far is $1-(\frac{1}{2})^{10}$.

Think about this math the next time you cut a pizza!