“Some people believe in imaginary friends. I believe in imaginary numbers.” R.M. ArceJaeger, American author
Igniting our imagination
We started Lazarus Math by building the number line. That started our journey through the integers. Then, as we added in rational numbers and irrational numbers, we included all real numbers. In the last section, we reviewed a subset of the integers, the prime numbers. As I was writing that section, I sensed prime numbers are a “complete set.” So, if we think about sets of numbers, we could think of the prime numbers, the integers, the rational numbers, and the irrational numbers. Of course, except for the prime numbers, we have both positive and negative versions of all these sets of numbers.
When we combine the rational and irrational numbers and form the bigger set, the real numbers, it allows us to draw a complete number line. We reviewed how there is no distance on the number line that we can measure that is not a real number. Perhaps that may seem obvious to you, but it is not trivial. Some of the greatest minds in math thought that the rational numbers formed the complete number line. But, as math people have proven it, we do not need to doubt that the real numbers cover the complete number line.
Does that mean that, as far as numbers go, the real numbers are the complete story? Notice the real numbers include all the other sets as subsets. It seems from a measuring perspective, we have everything we need with the real numbers.
Of course, life isn’t that simple for math people. You can think about math as a big story that begins with numbers. Great progress was made when we created the number line. We were already good with geometry, which appeals to our intuition because it uses common shapes. Then algebra appeared that abstracted our math even more. When the -coordinate system was developed, we were able to visualize some of the algebraic statements. But math is certainly more than measuring distances as we can do a lot of math that may or may not have anything to do with the world we live in. Measuring distances is only the beginning of what we want to do.
Let’s start with a real-life example and see where this simple story leads. We’re all familiar with a roller coaster. We can create a rough graph of the path of a roller coaster by using a parabola. Figure 1 is the graph for the simple parabola .
We can observe from the graph that if , then . However, for every other value of , the function returns a positive value. One of the great goals for math people is to solve for in an equation. So let’s consider a similar equation but fix the -value at -1. That produces this rather simple equation . This is not part of the parabola above since there are no negative results. What is the solution to this simple equation? It seems simple enough. Simply take the square root of both sides to get .
The professional answer math people gave for hundreds, even thousands, of years was that there is no solution. We can confirm that by punching -1 into the calculator and pressing the square root button. The result will be some sort of error.
To be honest, this is a bit embarrassing for us math folks. We make our living finding , but we can’t find a solution for in this simple equation . How did math people manage this embarrassment?
Math people can be strange. Yes, math people tend to be strict “rule followers.” They are not likely to “break the rules.” However, that doesn’t mean they sit idly by and let the calculator have the final word. Rather than break the rules, math people tend to change the rules. The rule is true that there is no solution. The catch is to specify that there is no solution for a real number . But why should great minds be limited to the confines of real numbers? We’ve recognized often in Lazarus Math that it requires imagination to do math. Math people were stuck in a dilemma in that they cannot find for such a simple equation. How unsettling! Since we can’t find a solution among the real numbers, let’s just imagine that there is a solution to this expression.
A new number
That means we need to imagine a new number, a number that is not a real number, that is a solution to this equation. What label or name should we give this new number? It doesn’t seem like we should label it a real number. That would be confusing since it is not a real number. Since we are just imagining all of this, why not let the new number be represented by ? That’s it, just lowercase .
On one hand, this isn’t anything too crazy. We’ve used letters before to notate special numbers, such as and . That was OK because this was just shorthand to represent a real number. We knew behind that letter was 2.718 and many digits. Our calculator confirms that. That leads to the question: what is the number ?
If we return to our previous equation and let the new number replace the previous unknown real number , then we can say that , or we can say that . Of course, the logical question is how. How is the solution to this equation ? We can’t see this solution on graph paper, and we can’t see this solution on our calculator. How does it work? It works because math people say it works. End of story. Kind of.
The math sandbox
This is the end of the birth story. But now, needs to live. If it’s going to survive, it must be able to play with the real numbers in a sandbox where is the only number that is not real, or at least not a real number. But once it is in the math sandbox, then it must play with the real numbers and not cause any major problems.
The way all this works is math people are free to define new things to come into the math sandbox. But once it is in the sandbox, they let go and the rules of the sandbox take over.
Before we let our new number go free and play, let’s give it a more formal name than just the nickname . It only seems appropriate that we call it an imaginary number. Yes, that works great. We create this new number with our imagination and classify it as an imaginary number.
That was easy. Of course, since we feel so empowered, we may be tempted to keep going and create another new number, perhaps a sibling for . We could call it for Junior. I’m sure we could find some use for it. But before we start planning for Junior, let’s see how our new baby does in the sandbox of real numbers.
We’re going to dive into the details of the math for . However, before we get into the weeds, let’s pause for a moment to convince you that making up new math isn’t anything new. Math people do it all the time.
Here are three examples you likely are already familiar with, and we have already discussed to some extent. These are examples of numbers that were not part of the math sandbox originally, and math people brought them in. I want to provide some details to these examples for context because it may seem wrong to you that we can make up an imaginary number. Also, I’m assuming you are not familiar with , so besides helping you understand how to use in math, I want to help you understand WHY we have in the first place. So I’m going to take things slowly to develop your intuition.
Made-up math example #1
Our first example is irrational numbers. We discussed these when we discussed the number line. They did not exist until math people wanted a solution for the length of the diagonal of a square. You may argue the square root of 2 exists because you can see a square in real life and the diagonal distance exists. But what is the length? We have no exact number for it. All we can say is if we multiply that number by itself, we get 2. We can only approximate the number. We can’t quantify the number exactly as a decimal. Like , does not exist on our calculator. We only have an approximate result, and that approximate result is a rational number. When we brought and the other irrational numbers into the math sandbox, we did not know their exact value. Like , we we wanted a solution to the equation . No solution existed among the known numbers. To appreciate how big a step this was, you must return to the time it did not exist.
I live in the United States of America, a relatively new country. The world evolved just fine without this country. But there were people in the 18th century that saw a problem and birthed a new country and a new system that would be a solution to that problem. It was a radical idea at the time and was met with opposition. Similarly, there was a time when bringing irrational numbers into the math sandbox was a revolutionary idea.
From our 21st century perspective, it may not seem like we are breaking any serious laws here because we know the number 2 exists and we know the operation square root exists and we know the operation square root on the number 4 exists. So it seems reasonable that we can apply this process to the number 2 even if we can’t quantify the result exactly. This probably feels like a small misdemeanor to us now.
Made-up math example #2
Our second example of made-up math is negative numbers. What is a negative number? The world operated just fine without negative numbers in the math sandbox. However, bringing negative numbers into the math sandbox doesn’t seem like a big deal either because we’re just taking the known numbers at the time and attaching a negative sign in front. But what is -3? Show me negative 3 apples. You can’t. Of course, it’s easy to think that negative numbers exist because they exist on our calculator and they exist in common areas of life. We certainly know in the state of Iowa that the temperature can dip below zero degrees. The weather person has declared the current temperature is -3 degrees. That temperature exists. If we overdraw our bank account, we have a negative balance. The bank will confirm the negative balance exists. Of course, we can draw a number line that goes left of 0 and observe the negative numbers bring a natural symmetry to the positive numbers.
However, because all these things are just ideas or scales we invented, the negative sign is arbitrary. We already have different scales for temperature with different definitions of when “negative” occurs. Regarding a negative bank balance, we can manage that with positive numbers using debits and credits. There is no such thing as a “negative” dollar bill. The number line is just a line to which we assign numbers, but it is just a line. How numbers relate to a line only exists in our mind.
Math people created negative numbers to complete our natural numbers. We accept these acts of creation because we are familiar with them. They are stories we have been told, and we eventually believed them. Let’s “give in” and allow negative numbers.
Made-up math example #3
Our third example is the result of multiplying two negative numbers. We know the answer: it is a positive number. We also have a calculator that will prove this to us, reinforcing our confidence this is true. Take a moment and think about it. How can, or better yet, why is negative 1 times negative 1 equal to positive 1?
This is another story we likely did not believe for quite a while. As far as breaking rules, this one may feel like a felony. However, there was a math teacher in our past that convinced us this was true, and we have believed that story ever since.
We can start with 3 marbles and add 3 more marbles to identify 6 marbles. We see multiplication at play by organizing these marbles in a 3 by 2 rectangle and observe marbles. But we already identified there is no such thing as minus 3 marbles. We multiply this by another number that doesn’t exist, -2, and somehow we believe the result is 6 marbles. That doesn’t make sense.
At first, this doesn’t make sense. But, at closer inspection, there is logic to it. The logic behind this is actually logic we need to understand how operates. So let’s dig further to make sure we understand why multiplying a negative number by a negative number is positive. Here is a familiar example to help us see why it makes sense that multiplying two negative numbers would result in a positive number.
Connecting to dance moves
Let’s recall our Straight x dance and the sequence, or steps, to produce our result.
Our first dance was Straight 1 where we moved left to right on the number line and eventually landed on the number . Figure 2 reviews this dance.
Remember all movement was left to right because all numbers were positive.
Eventually, we moved to a Straight -3.5 dance, and Figure 3 illustrates that dance.
Recall the first step was , which was a step in the positive direction since any number raised to 0 is 1. Then the second step was . The distance traveled remained 3.5, the same as in the Straight 3.5 dance. However, recall how we incorporated the negative value.
You can think of the step as , which is the same as (-1) times the step from the Straight 3.5 dance. Thus, multiplying by negative 1 produced the action of a turn on the number line. Now, consider the next step when . If we write it in the same format, we get or . Notice we are just multiplying -1 twice. What change resulted from ? We performed another turn which directed us from the negative direction toward the positive direction.
Can you recognize from our dancing experiment that it made sense for to be a positive result? It made sense because we assign the action of a turn when we multiplied by a negative number. Thus, when we perform two turns, it is the same as a full turn and we are again moving in the positive direction. The key concept to understand is to connect multiplying a number by a -1 is the same as a rotation on the number line. Then, when we multiply by -1 twice, we should rotate a turn twice which produces a full rotation back in the positive direction.
In summary, defining the result of multiplying two negative numbers to equal a positive number is something created by math people. It was motivated by the need to preserve patterns that were already in motion. This decision by math folks gave us a complete and consistent set of multiplication rules. Notice we are trying to preserve symmetry. We will take this concept to the logical next step with .
All 3 of these examples are things math people designed and invented. However, they appear factual because we have calculator keys that at least approximate these new rules. We know that if something makes it to the status of a calculator key, then it is a permanent tattoo in our math world. I’ve never seen a calculator with the imaginary number as an input. How can we visualize ?
Rules of the complex plane
First, we need a place to visualize . We have an -coordinate system, but that only involves real numbers. That is a problem we can overcome by inventing a different 2-dimensional plane. First, retain the -axis as the real numbers, but change the vertical axis to an axis that represents the imaginary numbers.
This is quite simple to do. Simply start with the normal -axis that consists of the real numbers and multiply each number by . I’ll explain in a moment what it means to multiply a real number by .
After converting our vertical axis to units of , the point becomes and the point becomes the point . We can follow the same pattern traveling down from the origin to the negative numbers. Moving down 1 unit from the origin lands at the point .
We call this the complex plane. You can think of the complex plane as similar to our normal -coordinate system except the vertical axis represent units of the imaginary number . In a sense, this is a sandbox the new must play in with the real numbers in order to survive. We’re finally ready to dig in and review some basics of imaginary numbers and the complex plane.
Plotting points on the plane
One easy way to get comfortable with the complex plane is simply to plot points on the complex plane in the same way we plot points on our normal -plane. The origin is in the middle with coordinates . The first number is based on the horizontal axis and the second number is based on the vertical axis, just like the -coordinate system. Now, the second part of this definition represents the imaginary component. If it helps, you can think of the origin as .
We have the land defined. Buckle up because you are ready to travel on this plane. Let’s plot 3 points.
First, plot . The real number is +1, so start from the origin and move 1 unit in the positive direction on the real axis, which is the horizontal axis. There is no imaginary component, so this is the point or , which is shown in Figure 4.
However, the complex plane is not just a collection of points. We can recast this plane with a different vision. The vision is to rewrite each point as a number. The number combines the real component and the imaginary component with addition. Thus, we can rewrite the point as the number , which we can simplify as 1 in this case since is 0. This is a change in our math and a bigger change in perspective. First, let’s practice the math with a couple more examples.
Next, plot . Now, there is no real component. From the origin, travel up two units to the point . What is the number connected with this point? Again, sum the components to get , or just .
Finally, plot . Notice we can find this point by starting at the previous point and moving 1 unit to the right, which represents a +1 real number. We could also arrive at the same point by starting at the first point and moving up 2 units to include the imaginary number. The number connected to the point is . We can’t simplify this any further.
When we convert a point in the complex plane to a number, we call it a complex number. Thus, all 3 numbers , , and are all complex numbers. If we have a point on the horizontal axis, the imaginary component of the complex number is 0, which produces only a real number. Likewise, if we have a point on the vertical axis, then the real component is 0. All other points on the complex plane produce a complex number that has a non-zero real component and a non-zero imaginary component.
Let’s take a step back and appreciate what just happened. We can now represent any point on the complex plane with a single number. If the plane was only in the real numbers, we needed an and -coordinate and a -coordinate. Thus, we defined a point by using two coordinates. In the complex plane, we can define a point using a single number. This may seem like a small step, but this pays huge “dividends” down the road. This is because we do operations on numbers, such as adding and multiplying. We can’t “multiply” two coordinates on the traditional -plane. But, if we identify how to multiply two complex numbers, then we can bring all the action of operations and apply it to this plane. The value of this will be revealed the more you use the complex plane. We’ll cover the basics to get you started.
Our first operation to consider is addition. How difficult is it to add numbers in the complex plane? As we navigate how this operation works, remember what a big deal this is. This may be the first time you “added” two points on a plane together. This is a big moment.
Adding points in the plane
Adding complex numbers is quite simple if you’re familiar with algebra. We manipulate the imaginary number similar to how we manipulate a variable in normal algebra. For example, , just like . Likewise, , just like .
Notice we already added the point to the point and arrived at the point . Observe the sum of the real components is the real component for the new point and the sum of the imaginary components is the imaginary component for the new point. Thus, we can add points simply by adding components. This is the same as converting both points to the complex number, then adding the complex numbers, and converting the complex number back to a point. For example, if we add the two complex numbers and , the result is . Then, converting this complex number back to a point, we arrive at the same point .
How do we add and , for example? Again, manage like it is variable even though is not a variable.
If we add and , we get since we can sum the real numbers and we can sum the coefficients of . Following the same strategy for the complex numbers, we get . That’s as far as we can go as we can’t simplify this result anymore.
Now, graph this result in Figure 5.
We have two inputs that we can find on the complex plane. We already found the point , so start here. Then, the action of adding to this number is the same as moving 3 units to the right in order to add the real component and moving 4 units up in order to add the imaginary component. We arrive at the point , which matches the algebraic result .
You can see that we can find this point by summing the real numbers and summing the imaginary numbers. Notice this has the same feel as adding numbers on a number line. The only difference here is we added a second dimension.
In short, adding points, or numbers, in the complex plane is an intuitive process. You can say we viewed addition from two perspectives. From an algebraic perspective, we simply added two complex numbers. From another perspective, we added two points in the complex plane and identified a third point. Both perspectives produced the same result.
Take a moment and appreciate what you just did. Before this, if you saw two points in a plane, you never would have thought about “adding the points” because the points were just coordinates, a location. I live in Des Moines, and you live at your point on the globe. Would we have thought about adding our locations to see where it landed? Now, on the complex plane, we have this new ability. We must think differently about what is a plane and how to move around on a plane. Also, because we can work with in a similar way we work with in algebra, we can say our imaginary number is playing well in the sandbox!
That is all you need to know to add complex numbers. What does it mean to multiply by a complex number?
Multiplying complex numbers
Remember the imaginary number came into the world through the operation of multiplication. Multiply by itself and we get -1. In other words, . This simple definition is the one building block to multiplying complex numbers. From here, we can use intuition to multiply any complex number we want.
For starters, rewrite as . We know any number times 1 is that number, so we know . It seems like is the same as . What is ? We know is . Thus, . What is ? Here, we can pair two sets of ’s as . That means .
Thus, we know and . Let’s complete the results for exponents 0 and 1. Anything raised to the 0 power is 1. Thus, . Of course, .
What is ? . How about what is ? . Now, let’s review our findings in order.
.
Notice as we increase our exponents beyond 6, we can always factor out as many as we want. Since and 1 is our multiplicative constant, we just have a continual pattern of what we saw when the exponents ranged from 0 to 4.
Remember on the vertical axis in our complex plane were different units of the imaginary number. The first unit is , the second unit up is which we can think of or as 2 times . In other words, multiplying a real integer number by is the same as repeated addition, which is consistent with how we view addition and multiplication for the real numbers. In other words, we can write or write and they are the same thing: 6. Thus, is the same as . It’s just that we can’t simplify the result any more than that.
Here is what we’ve identified so far regarding multiplying an imaginary number. If we perform repeated addition of an imaginary number, it is the same as multiplying by a real number the number of times we repeat the addition. In other words, .
Repeated multiplication of the imaginary number is raised to the number of times we performed the multiplication. This has the same effect as adding exponents. In other words, . Also, we can convert to -1 and to 1 if we have more than 1 repeated multiplication. This is all we need to know regarding the algebra of multiplying by . Let’s see how this plays out on the complex plane.
Multiplying by a real number
First, consider multiplying two positive real numbers in the complex plane. I’m going to walk through this slowly so we don’t miss any steps. Let’s say we start with a point on the plane, say . Since the component is 0, we remain on the real number line 2 units to the right of the origin. One of the benefits in using a complex plane is navigating is easy.
To create a navigation process, assume we always start at the origin, which is the point . Then, when we introduce the point , assume we are adding this point to the original point. Think of it as going for a walk. We must start somewhere. It’s easiest if we always start at the origin. Thus, once we mention the point , think of it as , which, of course, arrives at the point .
Now, rather than moving just 2 units to the right, we want to triple that distance. Thus, we could write , and we arrive at the point as shown in Figure 6.
Next, consider the result of multiplying by -3. What is ? When we moved from the origin to the point , you can think of it as moving two units to the right. In other words, we have a direction and we have a distance. When we multiplied it by a positive 3, we kept the same direction but changed the distance to 3 times 2 units, or 6 units. Think of the 3 as modifying the distance only, so rewrite -3 as . Thus, our movement is . Minus 1 gives us the instruction to make a turn from the direction we were going. We were going 2 units to the right before we scaled by the number 3. As a result, the distance we travel remains 6 since we have . But the direction changes to of a turn in the other direction. That means we move 6 units to the left and arrive at the point , which we illustrate in Figure 7.
Multiplying by i
Good. Now we are ready for the big move. What is ? Notice this time rather than multiplying by a real number, we are multiplying by the imaginary number. How can we interpret this move? Multiplying by also causes a change in direction just like multiplying by -1 produced a rotation. Can you guess the change in direction we get when we multiply by ?
Multiplying by produces of a rotation in the counterclockwise direction. That means we start at the origin and move 2 units in the direction we were moving before we multiplied by . If we multiply by , change the direction with a rotation. We were moving directly to the right, so a turn moves us straight up. That means results in moving 2 units straight up from the origin. Figure 8 illustrates we land on the point .
You may wonder why we assign a rotation to multiplying by . It may appear like an arbitrary rule. After all, came into the world to solve an algebra problem we didn’t have a solution for. It doesn’t seem intuitive that defining as the square root of -1 also translates to a of a rotation. That begs the question: where do we get the of a rotation?
Recall we explained why multiplying two negative numbers is a positive number by relating multiplication to a rotation on the number line. So, as we expand the number line to the complex plane, it almost seems intuitive that we rotate of a turn.
But we can get a better understanding of the of a rotation directly from the definition for . Remember our definition is . Apply this rule by changing one of the ’s to the point . What is the result of ? We can start at the origin and rewrite this as . If we don’t multiply by , then our action is to start at the origin and move up 1 unit. Now, when we multiply by , we make a rotation counterclockwise. That changes a 1 unit movement up to a movement 1 unit to the left. This lands on the point , or the number -1. This matches our algebra result of .
In fact, let’s take this result and multiply it by again. Thus, we can think of it as or . The first perspective is to change 1 unit to the left by a of a turn to 1 unit down, while the second perspective is to change a 1 unit up by two quarter turns, which results in a movement 1 unit down. Both arrive at the point . We know , which is consistent with our complex plane solution. The complete rotation is illustrated in Figure 9.
Multiplying by both real and imaginary
We reviewed multiplying by a real number 3 and an imaginary number . There are no surprises if we multiply by a number that has both a real and an imaginary component, such as . Thus, converts a movement 2 units to the right to a movement that has distance or 6. The direction changes by of a turn to go up, which lands on the point .
One more example should suffice. What is the result of ? Let’s review this in 3 steps.
Step 1: Without the multiplicative factor, we move 2 units to the right.
Step 2: Multiplying by the number 3 indicates we convert the distance of 2 units to 6 units. Now, we need the direction. The negative sign for the real number 3 is the same as multiplying by -1, which produces a turn, moving us in the opposite direction to the left.
Step 3: We also have an factor which produces two rotations that reverses us in the right direction. Thus, we land at the point .
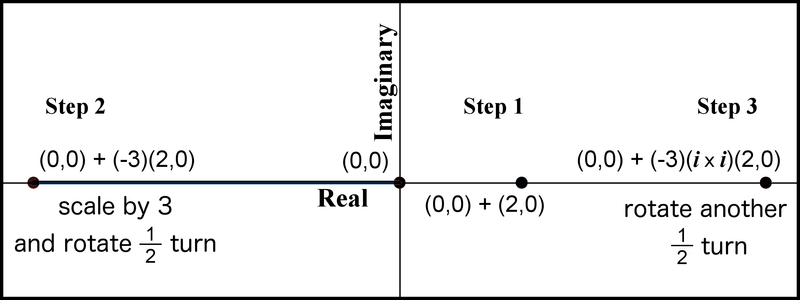
In short, the negative real number produced a of a rotation and multiplying by twice produced two rotations, or another rotation. The net impact of two rotations is a full rotation which moves us in the direction we started before all of this rotating, which is to the right. The complete story is documented in Figure 10.
Our baby has grown up
We started our story with a new number that was named imaginary. This was meant to be a derogatory term. Like most newborns, it has a humble beginning. It is the solution to the equation . It certainly was a small step. But as we nurtured the number and let it go, it played well with the real numbers in the complex plane. So much so we now define a new number, called a complex number, that simply uses addition and multiplication of the real numbers with this imaginary number. This complex number makes it even easier to operate in the complex plane. You can think of it as a marriage of the imaginary numbers with the real numbers. The form of this complex number is where and are real numbers. Now, we have this fascinating concept of a one number system. The one number system is the complex numbers. It is not just the real numbers and by itself. The complex numbers contain all the real numbers. Simply let and we have the real numbers. Let and and we have the imaginary number. For any other value for and , we mix real numbers with the imaginary. We can thank Euler and several other mathematicians in his era who saw the value of and the complex plane.
What is next?
All this movement on the complex plane may remind you of something we discussed in our “dancing” section. Recall we performed dances on the number line and on the -coordinate system as a way to identify where we finish after infinite steps of a dance. In the next section, we resume our dancing routine, so find your dancing shoes and play the music!















